ｙ=ｘ^3　の ｘ=１における接線とで囲まれた部分

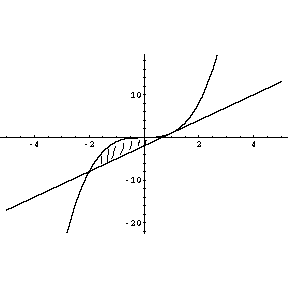
＜求積→面積について＞（公式など）

上記の部分の面積は次式で求められる

（一般的には次のような公式を使えばもっと簡単になる）

（４次関数と接線に囲まれた部分の面積）

上の曲線と直線（接線）で囲まれた部分の面積は以下の計算で求められる。


なお、上記のように ｘ=α、βを接点とするとき、次の公式で算出できる。
　


因数分解して

＜２元一次の連立方程式＞
  ２ｘ+３ｙ=-4 ・・(1)
　3ｘ-2ｙ=7　　・・(2)
　
Solve関数を使って単純に解く（解法1）


　
逆行列を使って解く（解法2）




　
行列の乗算で解く（解法３）


LinearSolve 関数を使って解く（解法4）


＜３元一次の連立方程式＞
x-2y+z = -4・・(1)
3x+2y-z = 8・・(2)
-x+3y+5z = 0 ・・(3)
　
（解法１）


（解法2）




（解法３）


（解法４）


　
　
　

　Mathematicaについて
　
　微分方程式とMathematica
　
数学あれこれ
　
　
数学のページへ 　トップページへ