「微分方程式をMathematica で解く」
　
最初にお断りしておくが、以下の式・図は
　
「Mathematica 微分方程式（小林 道正著）」
　
を参考にさせていただいた。アニメーションはオリジナルである。
　
　

　
　





　
　

　
　


　

(初期値の違いによるグラフの例）

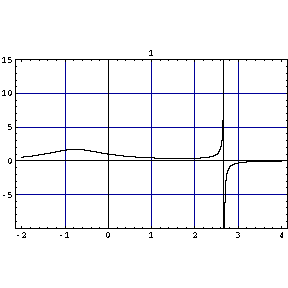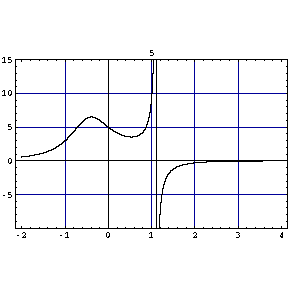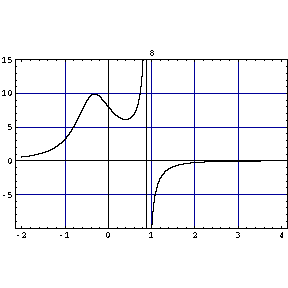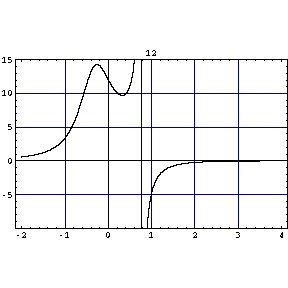
「変数分離形の微分方程式」の例

　y'=ax(b-y) の形　を解くと

　ａ＝ｂ=１，初期値をｙ（0）=ｋ としたとき、ｋ を変化させたときのグラフは次のようになる。
　
　

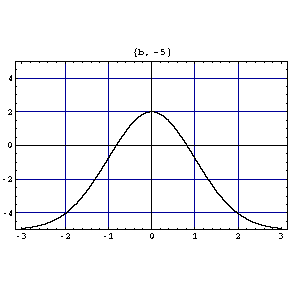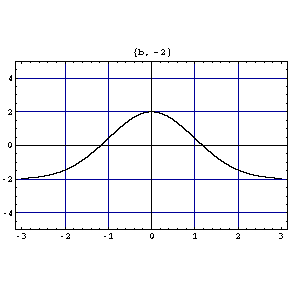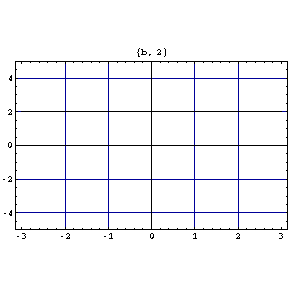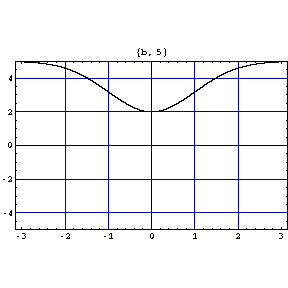
次に初期値を　y(0)=2、と固定して　ｂ の値を変えたときの解の変化を式とアニメーションで表してみると、
　

　
　
Mathematicaについて
　
高校数学とMathematica
　
数学あれこれ
　
数学のページへ　トップページへ